Fjarlægðarstiginn
Yfirlit
1. Kvörðun sólkerfisins – Hliðrunarmælingar
Hliðrunarmælingar, mælingar á fjarlægð með því að hliðra athugandanum, má rekja allt til tíma Eratosþenesar frá Alexandríu sem nýtti sér afstöðu sólar til að reikna ummál jarðarinnar. Frásagnir þeirra tíma herma að við ferðalag til borgarinnar Sýrene í Egyptalandi (sem nú er nærri Aswan) hafi Eratosþenes komið að brunni þar sem sólarljós náði aðeins að lýsa til botns á sumarsólstöðum, þann 21. júní ár hvert. Eratosþenes fylgdist ákaft með brunni nærri sínum heimaslóðum árin eftir en komst að því að sólarljósið náði ekki niður til botns á þeim sama degi. Með grófum mælingum gat hann áætlað að munur sólhæðar í Sýrene og í Alexandríu væri um það bil 7°. Eratosþenes þóttist vita að fjarlægðin milli Alexandríu og Sýrene væri 5.000 stadíur (lengd hins Ólympíska leikvangs, um 176 m) eða um 880 km, og gat því áætlað að þessar 7° spanni 880 km af ummáli hrings. Hann ályktaði því með réttu að ummál jarðar væri um það bil 45.260 km sem er ~ 20% frá réttu gildi. Til gamans má þó hugsa að ef til vill hafi Eratosþenes notað egypskt stadía, sem er um 157 m. Þá verður ummál jarðarinnar 40.400 km sem er innan við 1% frá réttu gildi. Hér hafði Eratosþenes notað aðferðir hornafræðinnar sem framhaldsskólanemar læra á fyrsta ári, til að reikna ummál jarðarinnar.
Um aldamót 16. og 17. aldar höfðu menn með hjálp þriðja lögmáls Keplers náð að njörva niður hlutfall sólkerfisins í mælieiningunni AU eða stjarnfræðieiningu, þ.e. vegalengdin milli jarðar og sólar. Vandamál þeirra tíma var hinsvegar að fá nákvæma mælingu á stjarnfræðieiningunni. Það var ekki fyrr en árið 1716 sem enski vísindamaðurinn Edmund Halley stakk upp á aðferð til að mæla þessa vegalengd með ágætri nákvæmni. Hann lagði til að mæla hliðrunarhorn sem sæist glöggt þegar Venus gengi fyrir sólina. Hliðrunin ætti að vera mælanleg ef grunnlínan milli tveggja athugenda væri nægilega löng. Athugendur staðsettir sitt hvoru hveli jaraðar ættu auðvelt með að greina þetta hliðrunarhorn. Halley lagði því grunninn að fyrstu hliðrunarmælingu sögunnar í stjarnvísindum og var hún framkvæmd árin 1761-69 þegar Venus gekk þvert fyrir sólina. Á mynd 1 sést hvernig hliðrunarmælingar eru notaðar til að meta á fjarlægð. Við mælanlegt hliðrunarhorn, p, og þekkta grunnlínu, B, má reikna fjarlægðina, d. Athugaðu að hér er gert ráð fyrir að lengri skammhlið þríhyrningsins og langhlið hans hafi sömu lengdina, d.
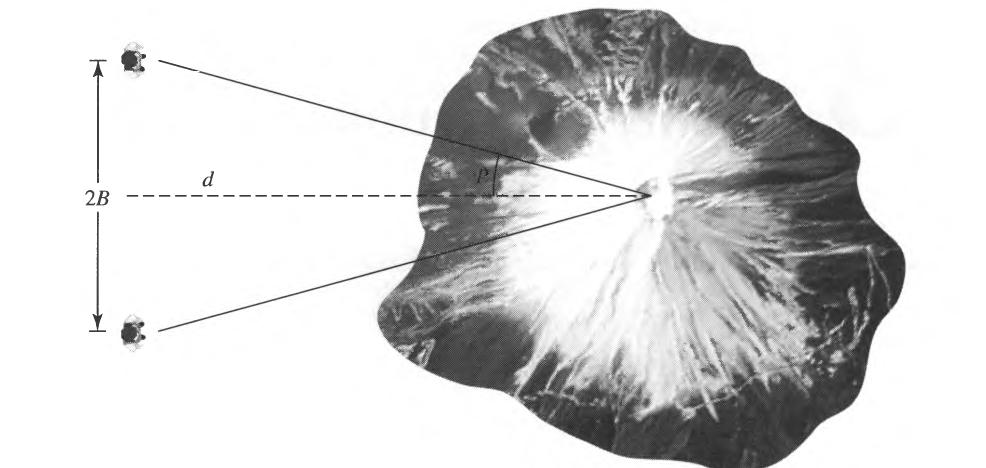 |
| Mynd 1: Hér sést hvernig nota má hliðrunarmælingar til ákvörðunar á fjarlægð. Mynd: Carroll & Ostlie (2007) |
| Reikistjarna | Fjarlægð í SE |
|---|---|
| Merkúríus | 0,387 |
| Venus | 0,723 |
| Jörðin | 1,000 |
| Mars | 1,524 |
| Júpíter | 5,203 |
| Satúrnus | 9,539 |
| Úranus |
19,182 |
| Neptúnus |
30,05 |
Sem fyrr segir fóru fram mælingar á þvergöngu Venusar árin 1761 og 1769 með hjálp sjónauka. Vísindamenn flykktust þá til tveggja heimsálfa svo grunnlína mælinganna væri jöfn þvermáli jarðarinnar. Niðurstöður mælinganna gáfu stjarnfræðieiningunni gildið 153.000.000 km. Sú skekkja sem upp kom í þessum mælingum hafa menn kennt svokölluðum dropahrifum um. Dropahrifin verða sennilega til í lofthjúpi jarðarinnar þegar fylgst er með þvergöngu innri reikistjarnanna og gera mönnum erfitt fyrir að skilgreina nákvæma tímasetningu á þvergöngunni. Um aldamótin 1900 gátu menn beitt stærri sjónaukum á smærri fyrirbæri og gátu því mælt hliðrunarhorn mun smærri eininga í sólkerfinu, svo sem smástirna. Því nær sem fyrirbærin eru því minni líkur eru á mæliskekkjum. Í dag hefur stjarnfræðieiningin verið mæld með nákvæmum ratsjármælingum og ber gildið 149.600.000 km. Nú þegar fjarlægð jarðar frá sólu var ákvörðuð var eftirleikurinn auðveldur fyrir menn að ákvarða fjarlægðir reikistjarnanna. Í töflunni hér til hliðar hafa fjarlægðir reikistjarnanna frá sólu verið settar upp sem hlutfall af SE.
2. Hliðrun fastastjarna
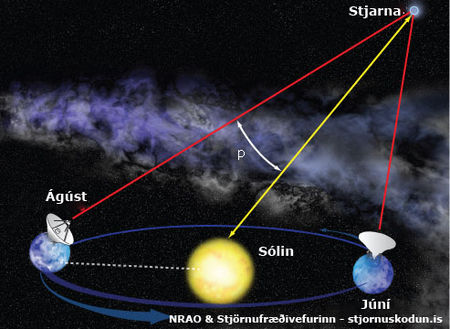 |
| Mynd 2: Fjarlægð til stjörnu mæld með hliðrunarmælginum. Grunnlína mælinganna er hér ein stjarnfræðieining. Mynd: NRAO & Stjörnufræðivefurinn. |
Til þess að eiga möguleika á því að nýta tækni hliðrunarmælinga á stærri skala en sólkerfið liggur beint við að stækka þurfi grunnlínu mælinganna. Lausn á því vandamáli var ekki auðleyst en vísindamenn nýta sér nú radíus sporbaugs jarðarinnar um sólu sem er, að sjálfssögðu, ein stjarnfræðieining. Hliðrunarmælingarnar eru þá framkvæmdar með 6 mánaða millibili sem gefur hliðrunarhornið líkt og áður. Á myndinni hér til vinstri má sjá hvernig hlutum er háttað við mælingu hliðrunarhorns á 6 mánaða fresti. Venja þykir í vísindum fjarlægðamælinga að mæla hliðrunarhornið, p, í bogasekúntum og hefur það valdið ýmsum erfiðleikum. Því kom fljótlega upp sú mælieining sem nefnd er parsekið. Nafnið parsek kemur af enska orðinu parsec sem er stytting á „parallax second“ og er tákn þess pc í einingakerfinu. Eitt parsek er sú fjarlægð til stjörnu sem hefur hliðrunarhorn upp á eina bogasekúntu. Eins og fyrr segir þá er staðsetning þeirrar stjörnu sem mæla á fjarlægð til mæld með 6 mánaða millibili og hliðrunarhornið ákvarðað. Þegar jörðin hreyfist á braut sinni um sólina virðist stjarnan hafa færst á himinhvelfingunni á þessum 6 mánuðum miðað við bakgrunnsstjörnur. Dæmigert hliðrunarhorn er t.d. 747,23 millíbogasekúntur, fyrir stjörnuna α-Kentár. Slíkt hliðrunarhorn samsvarar um 0,0002 gráðum og eru því ill greinanleg nema í sér til gerðum sjónaukum líkt og Very Long Baseline Array (VLBA) útvarpsjónaukunum eða í sér til gerðum ómönnuðum geimferjum.
2.2. Hipparcos
 |
| Mynd 3: Hipparcos geimfarið. Mynd: ESA |
Í ágúst 1989 var ómönnuðu geimfari Evrópsku geimferðarstofnuninnar (ESA), Hipparcos, skotið á loft. Helsta verkefni Hipparcosar var að safna upplýsingum um nákvæm hliðrunarhorn 118.000 mismunandi stjarna. Hipparcos var þeim eiginleikum gæddur að geta mælt hliðrunarhorn niður á 0,001 bogasekúntu eða því sem jafngildir fjarlægð allt að 1000 pc. Geimfarið notaðist við 29 cm Schmidt sjónauka sem varpaðiljósi á tvo samhallandi spegla sem sameinaði ljósið í einum brennipunkti. Speglarnir voru aðskildir með 58° og gáfu hvor um sig upplausn um 1° x 1°. Með þessum hætti var bæði hægt að framkvæma hliðranir á stórum sem smáum fleti á sama tíma. Í marsmánuði 1993 hafði Hipparcos safnað gögnum um 118.218 stjörnur og var þá verkefninu lokað. Á sínu fjögurra ára tímabili safnaði Hipparcos einnig ónákvæmum gögnum um milljónir annara stjarna sem nú hefur gefið vísbendingar til fjarlægða þeirra. Í dag hafa gríðarstór skjalasöfn verið gefin út sem afrekstur mælinganna, þar má nefna:
-
Hipparcos skráin (118,218 stjörnur)
-
Stjörnur úr Hipparcos skránni með upplýsingar um fjarlægð sem eru bjartari en birtustig 10,0 - fyrra skjal
-
Stjörnur úr Hipparcos skránni með upplýsingar um fjarlægð sem eru bjartari en birtustig 10,0 - seinna skjal
-
Tycho skráin (meira en 1,000,000 stjörnur)
-
Tycho-2 skráin (meira en 2,500,000 stjörnur)
2.3. GAIA
Sjá nánar: Gaia geimsjónaukinn
 |
| Mynd 4: Hugmynd listamanns á útliti GAIA geimfarsins. Mynd: ESA |
Bæði Geimferðastofnun Bandaríkjanna (NASA) og ESA hafa drög í höndum um nákvæmari fjarlægðarmælingar en Hipparcos leiðangurinn. Á teikniborði hefur ESA hönnun á geimfari sem nefnist GAIA. Höfuð verkefni GAIA er að kortleggja og ákvarða staðsetningu, fjarlægð og eiginhreifingar yfir milljónir stjarna á fimm ára tímabili. Geimfarið mun geta greint hliðrunarhorn niður á allt að 4 míkróbogasekúntur sem jafngildir fjarlægðarmælingu upp á 250.000 pc. GAIA mun framkvæma nákvæma könnun á stjörnum sem í nágreni sólar niður á birtustig 20 og hver stjarna er kortlögð allt að 70 sinnum á meðan verkefninu stendur. Geimfarið verður staðsett í svokölluðum Lagrange punkti L2 sem staðsettur er 1,5 milljón km fyrir utan braut jarðarinnar. Í þeim punkti skyggja hvorki sólin, jörðin né tunglið á þau fyrirbæri sem GAIA beinir sjónaukum sínum að.
3. Hreyfingar þyrpinga
Til að ákvarða fjarlægðir út fyrir vetrarbrautina þurfa fyrst að vera til góðar leiðir til að áætla fjarlægðir með beinum mælingum. Þau fyrirbæri sem hafa þann eiginleika eru oft kölluð fyrsta stigs fjarlægðarstikar. Ein af afburðaríkari leiðum til að áætla fjarlægðir innan vetrarbrautarinnar felst í því að greina hreyfingar stjörnuþyrpinga, svo sem Regnstirnisins í Nautinu og Sjöstirnisins. Þegar hreyfingar þyrpinga eru skoðaðar má sjá að allar stjörnur innan þeirra hreyfast sem ein heild þar sem þær eru allar bundnar saman vegna þyngdarkraftsins. Sé lína dregin frá hverri stjörnu í stefnu hreyfingarinnar má sjá að línurnar sameinast allar í einum samleitnispunkti. Til að líta á þetta í einfaldari mynd má hugsa sér að ef horft er eftir járnbrautarteinum sameinast hægri teinninn þeim vinstri í ákveðnum punkti í órafjarlægð. Á myndinni hér að neðan má sjá hvernig þessu er háttað fyrir Regnstirnið.
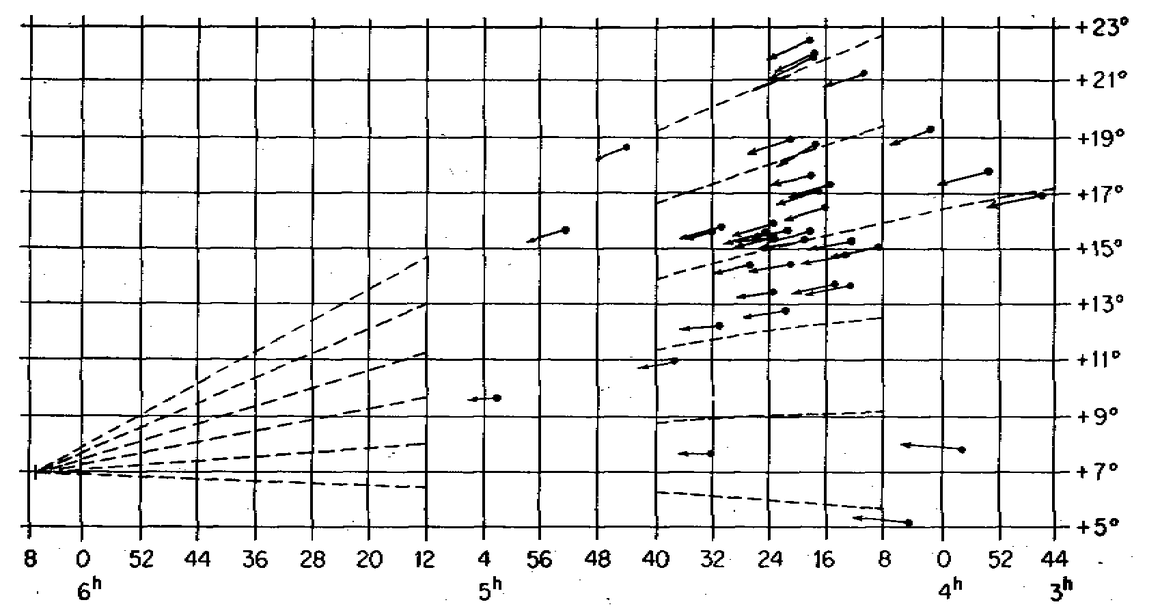 |
| Mynd 5: Hér hafa línur (eða stefnuvigrar) verið dregnar í stefnu hverrar stjörnu. Greinilegt er að þær stefna allar á einn samleitnispunkt. |
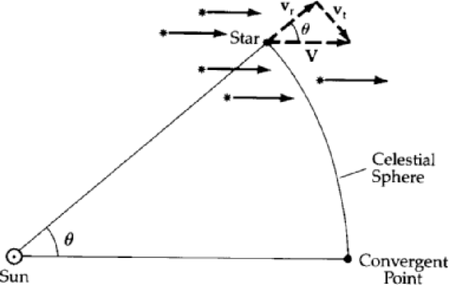 |
| Mynd 6: Hér má sjá hvernig áætla má horn milli sjónlínuhraða og þverhraða. |
Þar sem þyrpingar hreyfast sem ein heild í kring um vetrarbrautina má áætla fjarlægð til vetrarbrautarinnar með því að mæla hvert hornð sé milli sjónlínuhraða hennar (hraða þyrpingarinnar í sjónstefnu) og þverhraða. Hornið þar á milli má áætla að sé jafnt horninu milli hreyfingarstefnu sólarinnar og sjónlínu til þyrpingarinnar. Hreyfingar Regnstirnisins hefur verið notuð til að mæla fjarlægðina til hennar og voru niðurstöðurnar mjög í samræmi við hliðrunarmælingar einstaka stjarna sem fengnar voru með Hipparcos leiðangrinum. Fjarlægðin sem fékst var um 46 pc eða rúm 150 ljósár.
Hreyfingar stjörnuþyrpinga hafa nýst mjög vel til þess að meta reyndarbirtu meðlima stjörnuþyrpinga sem gefur þá möguleika á stilla meginraðir þyrpinganna sem nota má til langdrægnari fjarlægðamælinga.
4. Meginraðarmátun
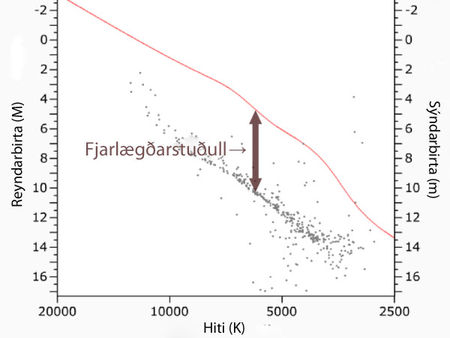 |
| Mynd 6: Hliðrun meginraðar óþekktrar þyrpingar við aðra þekkta gefur fjarlægðarstuðul. Mynd: |
Þegar fjarlægðir til stjörnuþyrpinga hafa verið ákvarðaðar er hægt að meta reyndarbirtu hvers meðlims til mikillar nákvæmni og þannig stuðla að nákvæmari fjarlægðamælingum með fyrirbærum sem teljast til annars stigs fjarlægðastika. Þegar fjarlægðin til Regnstirnisins hafði verið ákvörðuð með þokkalegri nákvæmni sáu menn sér fært að nýta sér aðferð litrófs-hliðranna á stærri fyrirbæri en áður. Litrófshliðrun felst í því að ákvarða megi reyndarbirtu (eða fjarlægð) út frá staðsetningu þeirrar stjörnu á meginröðinni. Aðferð meginraðarmátunar felst í grófum dráttum að teikna upp meginröð þekktrar stjörnuþyrpingar í reyndarbirtu annars vegar og meginröð þeirrar þyrpingar sem greina á í sýndarbirtu. Reiknuð er hliðrun þekktu þyrpingarinnar miðað við þá óþekktu og út fæst gróft mat á svokölluðum fjarlægðarstuðli óþekktu þyrpingarinnar. Þessi aðferð er sýnd á meðfylgjandi mynd, rauð lína táknar meginröð þekktrar þyrpingar.
5. Staðalkerti
Þegar mæla á fjarlægðir til fjarlægra vetrarbrauta getur það reynst þrautinni þyngri að gera sér í hugarlund hvernig taka eigi til hendinni. Staðalkerti eru fyrirbæri sem sitja í vetrarbrautum sem hafa þekkta reyndarbirtu (fast ljósafl). Það getur verið mjög vandasamt að velja staðalkerti, þau þurfa að uppfylla ýmis skilyrði, þ.á.m þurfa þau að
-
vera nægilega björt svo unnt sé að greina þau yfir órafjarlægðir
-
vera tiltölulega algeng í alheiminum
-
vera auðþekkjanleg, t.d. með ljósferlum eða lotum.
Ef eitthvert fyrirbæri væri með fasta reyndarbirtu yfir allt rúmið yrði það greinilega ákjósanlegasti fjarlægðarstiki sem til væri en, því miður, er þetta ekki raunin og því væri kannski heppilegra að tala um staðlanleg-kerti fyrir þau fyrirbæri sem við þekkjum.
5.1. Sefítar
Sjá nánar: Sefítar
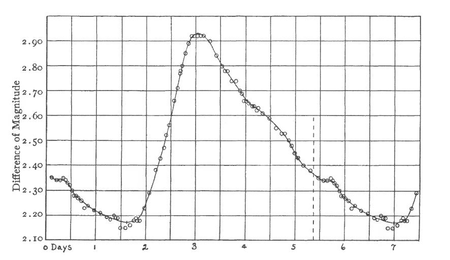 |
| Mynd 7: Sveifluferill stjörnunnar δ-Cephei, sefíta sem hefur sveiflulotu upp á 5,75 daga. Mynd: Sunsby University. |
Sefítar eru massamiklar sveiflustjörnur sem hafa sveiflutíma allt frá einum degi upp í hundrað daga. Kona að nafni Henrietta Swan Leavitt á heiðurinn af því að finna um 5% af þeim sveiflustjörnum sem fundist hafa á meðan hún vann við greiningu ljósmyndaplatna í Harvard háskólanum í Massachusetts. Leavitt upgötvaði um 2400 sefíta með sveiflutíma á bilinu 1 upp í 50 daga, nær allir af þeim eru staðsettir í Litla Magellanskýinu. Á myndinni hér að neðan má sjá hvernig birtustig δ-stjörnunnar í Sefeusi breytist með tíma. Við greiningu ljósmyndaplatnanna uppgötvaði Leavitt að síftar sem hafa hærra birtustig eru lengri tíma að fara í gegn um eina sveiflulotu.
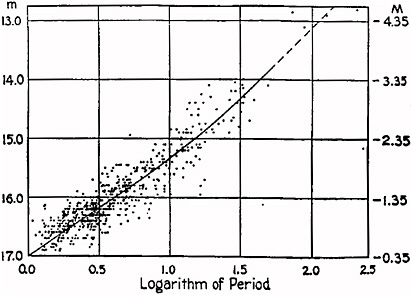 |
| Mynd 8: Sveiflulýsifall Leavitt. Greinilega sést að tengsl milli ljósmagns og sveiflu er nánast línulegt. Mynd: Caroll & Ostlie. |
Hún ákvað því að prófa að teikna sýndarbirtustig (m) stjarnanna sem fall af sveiflulotu (P) og tók eftir því að sambandið þar á milli er línulegt, eins og sjá má á mynd #! Leavitt hafði því hér uppgötvað sveiflulýsifall fyrir sefíta og lagt því grunninn að stöðlun þeirra. Nú þyrfti aðeins að meta hversu langan tíma fjarlægur sefíti fór í gegn um sveiflulotu, ákvarða út frá því reyndarbirtuna og þá er eftirleikurinn einfaldur. Sefítar hafa verið einn af helstu tólum stjarneðlisfræðinga enda má sjá fyrirbærin yfir fjarlægðir sem ná allt að 100 Mpc.
5.2. Spregnistjörnur Ia
Sjá nánar: Sprengistjörnur
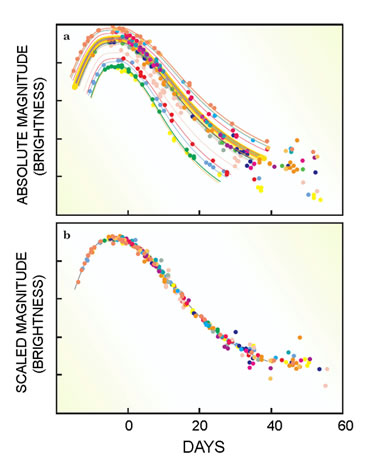 |
| Mynd 9: Hér má sjá hvernig ferlar nokkurra sprengistjarna hafa verið staðlaðir. Útkoman er einn staðlaður ferill sem nýta má í stöðlun sprengistjarna. |
Eftir þróanir á staðalkertum áttuðu menn sig fljótlega á því að til að mæla fjarlægðir á skala heimfræðinnar þyrftu menn að komast vel yfir getu sefítanna. Sprengistjörnur af gerð Ia hafa þann sterka eiginleika að vera gífurlega bjartar við hámark sitt á svokölluðum ljósferli (sjá mynd). Þegar sprengstjörnurnar eru skoðaðar kemur í ljós að þær eru vel staðlanlegar. Þegar sprengistjarna springur vex birta hennar stöðugt yfir eitthvert tímabil þar til hún nær hámarki, það tímabil getur tekið allt að 20 daga. Í hámarki nær reyndarbirta sprengistjörnunnar allt að mag 20 þar til hún dofnar aftur.Til þess að staðla þessi fyrirbæri hafa vísindamenn áttað sig á að því hraðar sem sprengistjarna nær hámarksbirtu sinni þeimur þrengri er birtuferillinn. Á myndinni hér til hliðar má sjá birtuferla nokkurra sprengistjarna táknaða með mismunandi litum. Ef teygt er á hverjum og einum þeirra er útkoman, líkt og sýnt er á neðri myndinni, einn staðlaður ljósferill. Almennt er talið að ljóferillinn hafi reyndarbirtu M = 19,3 pm 0,3 og því hægt að ákveða fjarlægðir til hýsilvetrarbrauta sprengistjarnanna með því að meta sýndarbirtu stig sprengistjörnunnar og ákvarða fjarlægðarstuðullinn.
Sprengistjörnur af gerð Ia gegna nú til dags veigamiklu hlutverki til ákvörðunar á ýmsum heimsfræðilegum fyrirbærum, til að mynda leit Hubblefastans, ákvörðunar á sveigju alheimsins og einnig „mesta klúðri“ Einsteins, heimsfastanum. Árið 1999 tókst tveimur óháðum rannsóknarhópum með hjálp sprengistjarna af gerð Ia að færa fram sönnun á því að alheimurinn sé ekki aðeins að þenjast út heldur sé hann einnig að hraða á sér. Sú niðurstaða hefur löngum verið kölluð mesta byting vísindanna á 20. öldinni. Nánar má lesa um þær uppgötvanir hér á Stjörnufræðivefnum.
6. Vetrarbrautir sem fjarlægðastikar
6.1. Tully-Fisher venslin
Árið 1977 uppgötvuðu stjarneðlisfræðingarnir Robert Tully og J.R. Fisher samband milli ljósmagns þyrilvetrarbrauta annars vegar og hámarks snúningshraða þeirra hinsvegar. Þessi vensl, sem hafa fengið nafnið Tully-Fisher venslin, komu í ljós þegar 21-cm ljómlína vetnis var skoðuð fyrir nokkrar þyrilþokur. Hægt er að skoða hvernig geislun frá ljómlínunni hliðrast í litrófinu eftir því hvort hún nálgast okkur eða fjarlægist vegna snúnings vetrarbrautarinnar. Því má segja að hliðrunin sé í beinu sambandi við snúningshraða hennar. Þriðja lögmál Keplers segir okkur einnig að massi vetrarbrautarinnar sé nátengdur snúningshraða hennar. Við getum enn haldið áfram því þeimur massameiri sem vetrarbrautir er því fleirri stjörnur hýsir hún og þeimur bjartari eru þær. Við getum því óhikandi sagt að hliðrun 21-cm vetnislínunnar sé nátengd ljósmagni þyrilvetrarbrauta. Á jörðu niðri er hægt að mæla þessar hliðranir mjög nákvæmlega og því er hægt að ákvarða reyndarbirtu fjarlægra vetrarbrauta og reiknað út fjarlægðina til þeirra.
6.2. Grunnsléttan
Fyrir sporvöluvetrarbrautir er ekki hægt að beita aðferð Tully og Fishers vegna þess að sporvöluvetrarbrautir snúast ekki. En árið 1987 benntu tveir amerískir stjarneðlisfræðingar, Marc Davis og George Djorgovski, á bein tengsl milli sýndarþvermáls sporvala, hreyfingu stjarna í þeim og yfirborðsskærleika þeirra. Þessi tengsl stærðar, hraða og skærleika hafa verið kölluð grunnsléttan vegna þess að í rúmfræði skilgreina þrír punktar plan (eða sléttu). Með því að mæla sýndarþvermál vetrarbrautarinnar og hraðadreyfingu stjarnanna geta stjarneðlisfræðingar reiknað út raunverulega stærð hennar.
7. Lögmál Hubble
Sjá nánar: Útþensla alheimsins og lögmál Hubbles.
Á þriðja áratug síðustu aldar voru menn önnum kafnir við að rannsaka eiginleika og gerð vetrarbrauta í þeirri von um að komast að niðurstöðu hvort þessar gasþokur væru hluti af vetrarbrautinni okkar eða aðskild kerfi. Þessar mælingar fóru fram með þeim hætti að rannsaka ljómlínur vetrarbrautanna til að ákvarða Doppler-hrif þeirra. Stjarneðlisfræðingur að nafni Vesto Slipher skráði niður mælingar á 40 vetrarbrautum og komst að því að nánast allar þeirra vetrarbrauta sýndu rauðvik í litrófi sínu og voru því að fjarlægjast Sólu. Árið 1925 komst Edwin Hubble að þeirri niðurstöðu með fjarlægðarmælingum á sefítum að Andrómeduvetrarbrautin, M31, var í raun svo langt í burtu að hún hlaut að vera stakt kerfi fyrir utan vetrarbrautina okkar. Hubble leitaði einnig að sefítum í fleirri vetrarbrautum og áttaði sig á því að burtfararhraði vetrarbrautanna hækkaði með fjarlægð. Árið 1929 birti Hubble niðurstöður sínar og leit þá lögmál Hubble fyrst dagsins ljós. Lögmálið má skrifa mjög auðveldlega með formúlunni
v_{0}H_{0} = d
Þar sem
- v0 er burtararhraði vetrarbrauta.
- H0 er Hubbles fastinn.
- d er fjarlægð til vetrarbrauta.
Með lögmáli Hubbles geta stjarneðlisfræðingar áttað sig á fjarlægðum sem ná vel yfir 1000 Mpc (>109 ljósár) svo lengi sem hægt er að ávkarða rauðvik (eða burtfararhraða) vetrarbrauta.
Tengt efni
Heimildir
- Carroll, B. W. og D. A. Ostlie (2007). An Introduction to Modern Astrophysics. Addison Weasley
- Freedman, Roger og Kaufmann, William. 2004. Universe, 6th Edition. W. H. Freeman, New York.
- Peacock, J. A. (1999). Cosmological Physics. Cambridge.
- Rowan-Robinson, M. (1986). The Cosmological Distance Ladder. Freemann.
- Ryden, B. (2003). Introduction to Cosmology. Addison Weasley.
Hvernig skal vitna í þessa grein
- Tryggvi Kr. Tryggvason (2010). Fjarlægðarstiginn. Stjörnufræðivefurinn. http://www.stjornuskodun.is/fjarlaegdarstiginn (sótt: DAGSETNING).
