Hornbil og hornstærðir

Gráður, bogamínútur og bogasekúndur

Horn er bilið milli tveggja lína sem mætast í punkti. Hornmál lýsir stærð horns nákvæmlega og grunneining þess er gráða, táknuð með °. Heilum hring er skipt í 360° og rétt horn mælist 90°.

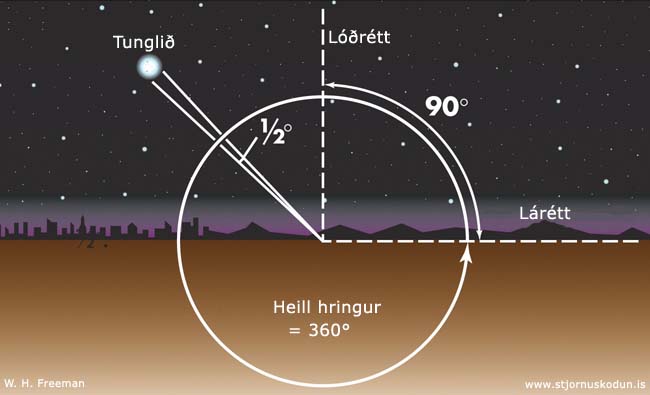Horn eru mæld í gráðum (°). Í heilum hring eru 360° og 90° í réttu horni. Hornið milli punktsins beint ofan við þig (lóðrétt) og sjóndeildarhringsins (lárétt) er 90°. Hornstærð tunglsins (stærð þess svæðis á himninum sem tunglið þekur) er ½°. Mynd: W. H. Freeman og Stjörnufræðivefurinn.

Stjörnufræðingar og stjörnuáhugamenn segja oft að tvær stjörnur séu um fimm gráður frá hvor annarri. Það þýðir að ef ímyndaðar línur væru dregnar frá augum athuganda, þar sem hann stendur í miðju ímyndaðs hrings, til hvorrar stjörnu, myndu línurnar tvær mynda fimm gráðu horn við augu hans. Þannig er fjarlægðin milli leiðarstjarnanna Dubhe og Merak í Karlsvagninum (Stórabirni) fimm gráður. Þessar stjörnur eru kallaðar leiðarstjörnur því þær benda beint á Pólstjörnuna í Litlabirni.

Þegar sagt er að stjarna sé 90° yfir sjóndeildarhring er hún beint fyrir ofan höfuð athugandans. Stjarnan myndar þá rétt horn á himninum miðað við athugandann og sjóndeildarhringinn.

Stjörnufræðingar nota hornmál einnig til að lýsa sýndarstærð (apparent size) fyrirbæra himinsins – það er að segja hversu stóran hluta himinsins fyrirbærið virðist þekja eða ná yfir. Þannig er sýndarstærðin eða hornið sem fullt tungl nær yfir á himninum um ½°. Við segjum þá að hornstærð tunglsins sé ½°. Þannig gætu tíu full tungl komist fyrir á svæðinu milli stjarnanna Dubhe og Merak.

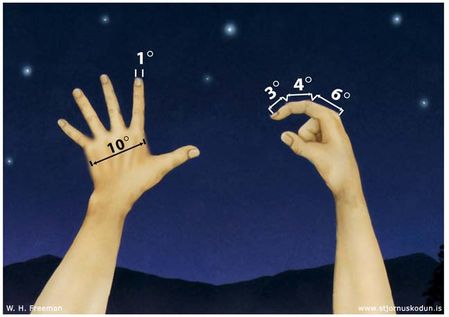
Hægt er að meta hornstærðir og hornbil milli fyrirbæra á himninum með hjálp útréttar handar fullorðins manns. Handabakið nær þannig yfir um 10° af himninum á meðan fingurbjörgin er um 1°. Hægt er að nota alla hluta vísifingurs í útréttri hendi til að meta nokkur mismunandi hornbil eða hornstærðir.

Gott er fyrir stjörnuáhugamenn að læra þessa aðferð. Ef þú kannt hana er mun auðveldar og fljótlegar að finna tiltekin fyrirbæri á himninum út frá stjörnukortum. Einnig getur skilningur á hornbili og hornstærðum hjálpað stjörnuáhugamanni við að finna réttu stækkunina í stjörnuskoðun.

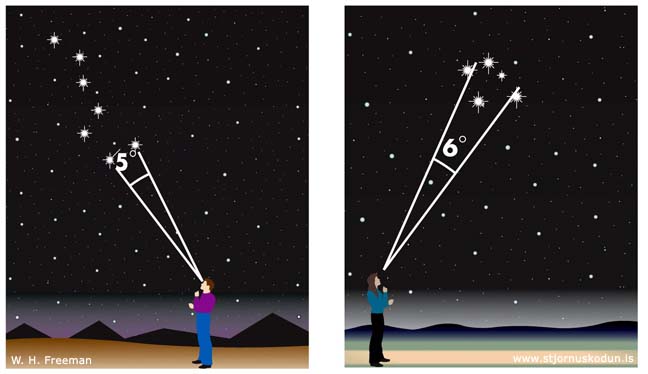Sjö björtustu stjörnurnar sem mynda Karlsvagninn (hluta Stórabjörns) sjást hvaðanæva að af norðurhveli jarðar. Hornbilið milli leiðarstjarnanna Dubhe og Merak í merkinu er um 5° en þessar stjörnur benda á Pólstjörnuna í Litlabirni. Fjórar björtustu stjörnurnar í Suðurkrossinum sjást einnig hvaðanæva að af suðurhveli jarðar. Hornbilið milli stjarnanna sem benda á suðurpól himins er um 6°. Mynd: W. H. Freeman og Stjörnufræðivefurinn

Bogamínútur og bogasekúndur

Á himinhvelfingunni eru tunglið og sólin þau fyrirbæri sem hafa mesta sýndarstærð, þó svo að hornstærð þeirra sé ekki nema ½°. Eins og við vitum og sjáum á næturnar ersýndarþvermál stjarnanna miklu minna en tungls og sólar og því langt innan við eina gráðu. Til þess að skilgreina smærri horn skiptum við einni gráðu í 60 bogamínútur (hornmínútur) sem táknaðar eru með ', til dæmis 60'. Bogamínúta er mjög smá eining en þó of stór til að mæla stjörnurnar. Því er til enn smærri eining sem kallast bogasekúndur (hornsekúnda) og er táknuð með ". Í einni bogamínútu eru 60 bogasekúndur líkt og í hefðbundinni mínútu. Þar af leiðandi gildir:

1° = 60 bogamínútur = 60'
1' = 60 bogasekúndur = 60''

Ein bogasekúnda er 1/3600 hluti úr gráðu og 1/1296000 hluti úr hring. Í þessari mjög smáu einingu mæla stjörnufræðingar greinigæði augna og sjónauka, hornbilið milli tvístirna og sýndarþvermál reikistjarna og djúpfyrirbæra.

Sem dæmi má nefna að ef fjarlægð milli tveggja fyrirbæra á himninum væri fjórði hluti úr gráðu er sagt að fjarlægðin milli þeirra sé 15 bogamínútur (60/4 = 15). Björtustu reikistjörnunnar eru aftur á móti oftast einungis nokkrar bogasekúndur að þvermáli. Sem dæmi má nefna að 1. janúar 2004 var sýndarþvermál eða hornstærð Satúrnusar aðeins 20,6 bogasekúndur frá jörðu séð. Þetta er svo lítil stærð að engin leið er að sjá nokkur smáatriði á Satúrnusi, til dæmis hringana, án þess að nota stjörnusjónauka. Sjónaukinn stækkar þá sýndarþvermál Satúrnusar. Væri spegill sjónauka 10 sentímetrar að þvermáli gæti hann greint smáatriði sem væru aðeins 1 bogasekúnda að stærð. Þetta jafngildir því að geta greint breidd krónupenings í 4 km fjarlægð. Því stærra sem ljósop sjónaukans er, því betri eru greinigæðin og því meira sést í gegnum sjónaukann.

Ef við þekkjum hornstærð tiltekins fyrirbæris, sem og fjarlægðin til þess fyrirbæris, getum við reiknað út raunstærðina með mjög einföldum hætti.

Smáhornsformúlan

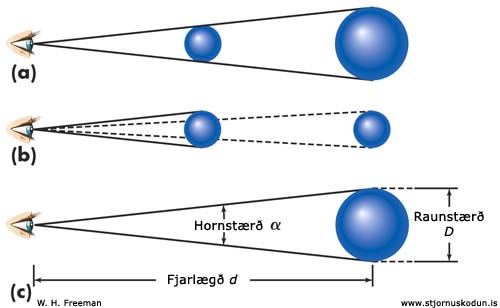(a) Tvö fyrirbæri með sömu hornstærð geta haft mismunandi raunstærð ef þau eru í mismikilli fjarlægð frá athugandanum. (b) Hornstærð fyrirbæris er meiri því nær sem það er athugandanum. (c) Smáhornsformúlan lýsir raunstærð fyrirbæris D miðað við hornstærðina α og fjarlægð þess frá athuganda d. Mynd: W. H. Freeman og Stjörnufræðivefurinn

Eins og áður sagðu er hægt að meta hornbil fyrirbæra á himninum með höndunum og fingrunum. Með nokkuð einföldum búnaði geta stjörnufræðingar mælt hornstærðir upp á brot úr bogasekúndu.

Mikilvægt er að hafa í huga að hornstærð er ekki það sama og raunstærð. Þannig getur þú hæglega hulið tunglið með þumalfingrinum í útréttri hendi (eins og Tom Hanks gerði í Apollo 13). Tunglið er þó vitaskuld miklu stærra en þumalfungurinn, en þumalfungurinn er miklu nær.

Á myndinni hér fyrir neðan sést hvernig hornstærð fyrirbæris tengist raunstærðinni. a sýnir að fyrir einhverja gefna hornstærð er raunstærð þess meiri því fjarlægara sem fyrirbærið er. Áðurnefndur þumalfungur er ágætt dæmi þar sem hann hefur um það bil sömu hornstærð og tunglið, en tunglið er miklu fjarlægara og hefur því miklu meiri raunstærð. b sýnir að fyrir gefna raunstærð minnkar hornstærðin því fjarlægara sem fyrirbærið er. Þess vegna virðist bíll smám saman minnka því meira sem hann fjarlægist.

Við getum lýst þessum athugunum stærðfræðilega í smáhornsformúlunni:

D = α d / 206.265

þar sem

D = raunstærð fyrirbærisins

α = hornstærð fyrirbærisins í bogasekúndum
d = raunveruleg fjarlægð til fyrirbærisins í km

Talan 206.265 er fasti og jafngildir fjölda bogasekúnda í heilum hring (360°) deilt með 2π (hlutfallinu milli ummáls og radíus hrings).

Tökum dæmi. Þann 26. júlí 2003 var Júpíter í 943 milljón km fjarlægð frá jörðinni og hafði hornastærðina 31,2 bogasekúndur. Hvert er raunverulegt þvermál Júpíters?

Vitum:

D = ?
α = 31,2'' (bogasekúndur)
d = 943.000.000 km

D = 31,2 x 943.000.000 km / 206.265 = 143.000 km

Svarið okkar er mjög nærri lagi því raunverulegt mælt þvermál Júpíters er 142.984 km.

Tökum annað dæmi. Við góðar aðstæður á jörðinni getur sjónauki greint smáatriði sem eru aðeins um 1 bogasekúndu að stærð. Hver er mesta fjarlægð þar sem hægt er að greina smáatrði á stærð við mann sem er um 1,7 m á hæð við slíkar aðstæður?

Vitum:

D = 1,7 m
a = 1'' (bogasekúnda)
d = ?

d = 206.265 x 1,7 m / 1 = 350.000 m = 350 km

Svarið okkar sýnir að þessi vegalengd (350 km) er innan við 1/1000 af raunverulegri vegalengd til tunglsins (384.000 km). Þar með höfum við sýnt fram á að jafnvel stærstu og bestu stjörnusjónaukar jarðar gætu ekki greint geimfara á yfirborði tunglsins.

Maður með fullkomna sjón (20/20) getur greint eins bogamínútu bil milli tveggja punkta í sex metra fjarlægð.

Heimild:

1. Freedman, Roger og Kaufmann, William. 2004. Universe, 7th Edition. W. H. Freeman, New York.

Hvernig vitna skal í þessa grein

• Sævar Helgi Bragason (2010). Hornbil og hornstærðir: Gráður, bogamínútur og bogasekúndur. Stjörnufræðivefurinn. http://www.stjornuskodun.is/alheimurinn/stjornur/hornbil-og-hornstaerdir (sótt: DAGSETNING).