Svarthlutargeislun

Grunnhugmyndin er sáraeinföld. Ímyndaðu þér hlut sem gleypir hverja einustu ljóseind sem á hann fellur. Þessi hlutur væri fullkomlega svartur þegar hann er kaldur þar sem hann endurvarpar engu ljósi frá sér. Ljóseindir bera orku og því myndi hluturinn hitna þegar hann gleypir sífellt fleiri ljóseindir. Eina leiðin til þess að slíkur hlutur sé í jafnvægi við umhverfi sitt er ef hann geislar jafnmikilli orku frá sér og hann gleypir. Slík geislun, sem er varmageislun, kallast svarthlutargeislun og er háð hitastigi hlutarins. Svarthlutargeislun er litróf ljóss sem aðeins er háð hitastigi hlutarins, hvort sem um er að ræða stein, manneskju, stjörnu eða jafnvel alheiminn sjálfan.

Eðlisfræðilögmálin sem skýra svarthlutargeislun kallast lögmál Plancks. Svarthlutargeislun hefur ákveðna lögun, birtu og bylgjulengd sem færist samfara því að hitastig svarthlutarins breytist. Ef hitastig svarthlutarins eykst færist hámarksbirtan að styttri, blárri og orkuríkari bylgjulengdum, en ef hitastigið minnkar færist hámarksbirtan að lengri, rauðari og orkuminni bylgjulengdum. Þessi áhrif kallast tilfærslulögmál Wiens.

Sólin okkar er 5.500°C (5.800 K) heit og er björtust í gula hluta litrófsins. Heitari stjörnur eru bjartastar í útfjólubláa hlutanum. Jafnvel manneskjur, ég og þú, gefa frá sér svarthlutageislun; líkamshitinn er um 37°C (310 K) svo geislunin er mestmegnis í innrauðum bylgjulengdum (bylgjulengd þín er tíu míkrómetrar) sem er alltof lítil til þess að við gætum gefið frá okkur sýnilegt ljós.

Svarthlutargeislun er sannarlega óumdeild og er oft nefnd hér á Stjörnufræðivefnum. Hún er bjarmi sólar og ljósapera. Hún kemur frá fólki, reikistjörnum og köldum og dimmum gas- og rykskýjum í vetrarbrautum. Henni er oft lýst sem varmageislun og er sá hitamælir sem stjarnvísindamenn nota á alheiminn. Mælingar á litrófi svarthlutar gerir okkur kleyft að mæla hitastig í milljarða ljósára fjarlægð!

1. Ekki er allt gull sem glóir

Til þess að öðlast skilning á fyrirbærum næturhiminsins rannsaka stjörnufræðingar einkenni ljóssins sem berst frá þeim. Þessar rannsóknir eru mjög mikilvægar því þær leiða í ljós að mismunandi tegundir ljóss eða rafsegulgeislunar er venjulega tilkomin á mismunandi hátt.

Einfaldasta og algengasta leiðin til að framkalla rafsegulgeislun, annað hvort á jörðinni eða utan hennar, er að hita upp hlut. Heitur vír í ljósaperu gefur frá sér hvítt ljós á meðan neonskilti gefur frá sér rauðan bjarma þegar neongasið hitnar af völdum rafstraums. Á svipaðan hátt verður til næstum allt það sýnilega ljós sem berst okkur utan úr geimnum frá heitum fyrirbærum eins og sólinni og stjörnunum. Tegund og magn þess ljóss sem berst okkur frá heitu fyrirbæri segir ekki aðeins til um hversu heitt fyrirbærið er, heldur líka um aðra eiginleika þess. Við getum t.d. sagt til um hvort heitt fyrirbæri sé úr tiltölulega þéttu eða þunnu efni. Sjáðu til dæmis muninn á ljósaperu og neonskilti. Málmþráðurinn í ljósaperunni framkallar hvítt ljós sem er blanda allra lita eða bylgjulengda sýnilegs ljóss, á meðan þunna og gegnsæja neongasið býr til rauðleitt ljós sem þar af leiðandi hefur eina ákveðna bylgjulengd. Jafnvel þótt sólin og stjörnurnar séu úr gasi og séu ekki föst gefa þau frá sér ljós með mörgum af sömu eiginleikum og ljós sem berst frá föstum og glóandi hlut.

Ímyndaðu þér málmsuðumann sem hitar járnbita. Þegar járnið hitnar byrjar það að gefa frá sér djúprauðan lit eins og sjá má á myndinni hér fyrir neðan. (Þú getur séð þennan sama rauða lit úr járnvírnum í brauðristinni þinni.) Um leið og hitastigið hækkar byrjar járnið að gefa frá sér bjartara og appelsínugulleitara ljós. Við enn hærri hitastig verður ljósið bjartara og gulara. Gæti járnið hitnað enn frekar, án þess að bráðna og gufa upp, myndi það gefa frá sér bláhvítt ljós við hæsta hitastig.

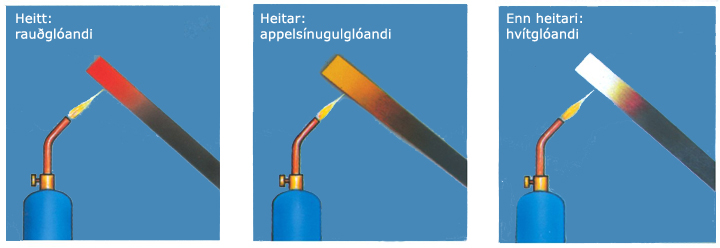Mynd 1: Myndaröð sem sýnir hvernig litur upphitaðs járnbita breytist með hækkandi hitastigi. Fyrst er járnið rauðglóandi, þá appelsínugulglóandi og loks gulhvítglóandi. Mynd: Freedman og Kaufmann (2004).

Þetta dæmi sýnir að sú bylgjulengd auk magni þeirrar orku sem heitt og þétt fyrirbæri gefur frá sér veltur á hitastiginu. Því heitara sem fyrirbærið er, því meiri orku geislar það frá sér. Þeim mun meiri sem orkan er, því styttri er bylgjulengdin þaðan sem mesta orkan berst. Köld fyrirbæri gefa frá sér tiltölulega litla orku sem þýðir að orkuútgeislun þeirra einkennist af löngum bylgjulengdum.

Þetta skýrir hvers vegna þú sérð ekki í myrkri. Hitastig fólks, dýra og húsgagna er miklu minna en hitastig upphitaða járnbitans á myndinni fyrir ofan. Þessir köldu hlutir geisla aðallega frá sér orku með lengri bylgjulengd en sýnilegt ljós, svokölluðu innrauðu ljósi. Augu okkar eru ónæm fyrir innrauðu ljósi og þess vegna sérðu hluti ekki í myrkvuðu herbergi. Þú gætir aftur á móti séð innrautt ljós með hjálp þar til gerðra myndavéla sem eru næm fyrir innrauðri geislun. 

Til þess að átta sig betur á sambandinu milli hitastigs þétts hlutar og geislunarinnar sem hann gefur frá sér, er gagnlegt að vita hvað átt er við með „hitastigi”. Hitastig efnis er háð hreyfiorku atómanna, þ.e.a.s. hraðanum sem atómin eru á. Ef eitthvað efni er heitt eru atómin í efninu á miklum hraða (árekstrar milli atóma örir sem hækka hitann) en ef efnið er kalt hreyfast atómin hægt (minna um árekstra). Vísindamenn tjá venjulega hitastig í Kelvin kvarðanum. Þar er hitastig mælt í kelvin (K) upp frá alkuli. Alkul er lægsta mögulega hitastig, mesta hugsanlega frost. Við alkul hreyfast atóm eins hægt og mögulegt er (þau geta aldrei stöðvast algjörlega). Á Celsíuskvarðanum er alkul (0 K) -273°C. Venjulegur stofuhiti er 293 K eða 20°C.

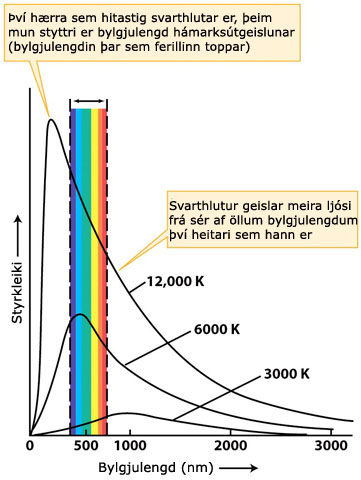Mynd 2: Ferlarnir þrír sýna ljósstyrk sem fall af bylgjulengd sem svarthlutur við tiltekið hitastig geislar frá sér. Regnbogabandið eru litirnir í sýnilega hluta rafsegulrófsins. Mynd: Freedman og Kaufmann (2004).

Myndin hér til hliðar sýnir hvernig geislun frá þéttu fyrirbæri er háð hitastigi þess í Kelvin. Hver ferill á myndinni sýnir ljósstyrkinn frá hverri bylgjulengd sem þétt fyrirbæri gefur frá sér við tiltekið hitastig: 3000 K, 6000 K og 12.000 K. Ferlarnir sýna, með öðrum orðum, litróf ljóssins sem berst frá slíku fyrirbæri. Við tiltekið hitastg gefur þétt fyrirbæri frá sér geislun á öllum bylgjulengdum svo litróf þess er sléttur samfelldur ferill án nokkurra eyða.

Lögun litrófsins veltur hins vegar á hitastiginu. Fyrirbæri með tiltölulega lágt hitastig, t.d. 3000 K, hefur lágan feril sem bendir til þess að styrkur geislunarinnar sé tilölulega lágur. Bylgjulengd hámarksútgeislunar, þar sem ferillinn hefur hápunkt og útgeislun sterkust, er stutt. Því hærra sem hitastigið er, því hærri er ferillinn (sem bendir til meiri styrks) og því styttri er bylgjulengd hámarksútgeislunar.

Myndin hér fyrir ofan sýnir að bylgjulengd þétts, 3.000 K heits fyrirbæris, er í kringum 1.000 nm (1 míkrómetri). Þar sem þetta er innrauð bylgjulengd, utan sýnilega hlutans, gætir þú eflaust haldið að þú sjáir ekki geislunina frá þessu fyrirbæri. Ferillinn sýnir aftur á móti að þetta fyrirbæri geislar líka heilmiklu ljósi frá sér í sýnilega hlutanum, svo bjarminn frá fyrirbærinu er greinilegur. 

3.000 K ferillinn er nokkru hærri við rauða enda sýnilega hluta litrófsins en við fjólubláa endann. Við þetta hitastig er fyrirbærið því rautt á litinn. 12.000 K ferillinn sýnir að hámarksútgeislunin er í útfjólubláa hlutanum, með styttri bylgjulengd en sýnilegt ljós, svo heitt fyrirbæri gefur líka frá sér heilmikið magn sýnilegs ljóss, miklu meira en hlutir sem eru 6.000 K eða 3.000 K heitir, og fer því varla framhjá nokkrum manni. Ferill 12.000 K heits fyrirbæris er hæst við bláa endan svo litur þess er blár eða bláhvítur. Þessar niðurstöður eru í fullkomnu samræmi við litabreytingar hitaða járnsins á myndinni fyrir ofan. Sama lögmál gildir um stjörnur. Stjarna eins og Vega í Hörpunni er blá á litinn vegna þess að hún er mjög heit, á meðan stjarna eins og Betelgás í Óríon er rauðleit vegna þess að hún er miklu kaldari.

Þessar athuganir leiða til almennrar reglu sem er mikið notuð þegar hitastig stjarna og reikistjarna er skoðað:

Því hærra sem hitastig hlutar er, því sterkari rafsegulgeislun gefur hann frá sér og bylgjulengdin styttri þar sem geislunin er mest.

2. Svarthlutur og svarthlutargeislun

Ferlarnir á myndinni eru dæmi um þétta og heita hluti sem kallast svarthlutir. Fullkominn svarthlutur endurvarpar ekki neinu ljósi, en gleypir þess í stað alla þá geislun sem á hann fellur. Útgeislun svarthlutar er þar af leiðandi að öllu leyti afleiðing hitastigs hans. Dæmigerðir hlutir úr daglegu lífi eins og borð, tölva, stóll og menn, eru ekki fullkomnir svarthlutir enda endurvarpa þeir ljósi sem skýrir hvers vegna við sjáum þá. Sólin hegðar sér að miklu leyti eins og fullkominn svarthlutur því hún dregur í sig næstum alla þá geislun sem á hana fellur utan frá. Ljósið sem svarthlutur gefur frá sér kallast svarthlutargeislun og ferlarnir á myndinni fyrir ofan nefnast svarthlutaferlar. Örbylgjukliðurinn hefur næstum fullkominn svarthlutaferil.

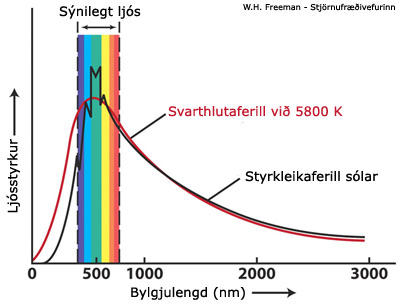Mynd 3: Grafið sýnir svarthlutaferil hlutar við 5800 K og styrkleikaferil sólar. Eins og sjá má falla báðir ferlarnir mjög nærri hver öðrum. Á þennan hátt getum við fundið út hversu heit sólin okkar er. Mynd: Freedman og Kaufmann (2004).

Hafðu í huga að svarthlutur þarf alls ekki að vera svartur á litinn, þótt hann kallist svarthlutur. Sólin er augljóslega ekki svört, en það er vegna þess að hitastig hennar er svo hátt að hún skín skært. Við stofuhita væri svarthlutur mjög svartur. Jafnvel þótt hann væri jafn stór sólinni gæfi hann aðeins frá sér 1/100.000 af orkunni. Svarthlutaferill slíks hlutar er alltof lítill til þess að sjást á grafinu á myndinni fyrir ofan. Auk þss væri mestur hluti geislunar af þessu tagi langt utan þess sviðs sem augun í okkur greina.

Myndin hér til hliðar sýnir svarthlutaferil 5.800 K heits hlutar og styrkleikaferil sólarljóssins eins og það mælist utan úr geimnum (lofthjúpurinn dregur ákveðnar bylgjulengdir í sig svo nauðsynlegt er að mæla styrkleikann utan úr geimnum). Hápunktur beggja ferla er nærri miðju sýnilega litrófsins, við 500 nm bylgjulengd. Taktu eftir hversu nálægt svarthlutaferillinn er mælda styrkleikaferlinum. Þetta sýnir að hitastig sólar er um 5.800 K. Á þennan hátt getum við fundið út hversu heit sólin, reikistjörnur og sólstjörnur eru, þótt þau séu órafjarri.

Þessi nánu tengsl milli svarthlutarferils og mælds styrkleikaferils er lykilástæða þess að stjörnufræðingar hafa áhuga á eðlisfræði svarthlutargeislunar. Svarthlutargeislunin veltur eingöngu á hitastigi hlutarins en ekki efnasamsetningu hans. Ljós sem bráðið gull gefur frá sér við 2.000 K er mjög nálægt því að vera hið sama og bráðið blý gefur frá sér við sama hitastig. Þrátt fyrir það geta stjörnufræðingar líka fundið út efnasamsetninguna – taka fingraförin ef svo má segja – með því að skoða ljósið frá stjörnu. Myndin hér til hliðar sýnir á hinn bóginn að styrkleikaferill sólar er ekki nákvæmlega eins og svarthlutaferillinn. Munurinn milli litrófs stjörnu og svarthlutar gerir okkur kleyft að finna út efnasamsetninguna, eins og lesa má um í umfjöllun okkar um litrófsgreiningu.

Sjá nánar: Litrófsgreining

3. Lögmál Wiens og Stefan-Boltzmann

Stærðfræðiformúlan sem lýsir svarthlutaferlunum er tiltölulega flókin. Aftur á móti eru til tvær einfaldar formúlur fyrir svarthlutageislun sem hafa reynst mjög gagnlegar á hinum ýmsu sviðum stjörnufræðinnar. Stjörnufræðingar nota þær til þess að rannsaka stjörnur og reikistjörnur (sem eru þétt en fremur köld fyrirbæri sem gefa frá sér innrauða geislun). Ein af formúlunum tengir hitastig svarthlutar við bylgjulengd hámarksútgeislunar, en hin tengir hitastigið við orkuna sem svarthlutur geislar frá sér.

3.1. Lögmál Wiens

Myndin af svarthlutaferlunum sýnir að því hærra sem hitastig (T) svarthlutar er, því styttri er bylgjulengd hámarksútgeislunar (λ_max). Árið 1893 nýtti þýski eðlisfræðingurinn Wilhelm Wien hugmyndir sínar um hita og rafsegulmagn til þess að gera þetta samband magnbundið. Formúlan sem hann leiddi út, sem við í dag köllum lögmál Wiens, er

\lambda_{max} = \frac{0,0029 \textrm{K m}}{T}

þar sem λ_max = bylgjulengd hámarksútgeislunar hlutarins (í metrum) og T = hitastig hlutarins (í kelvingráðum).

Lögmál Wiens segir að mjög heitir hlutir geisla mest frá sér á stuttum bylgjulengdum; þeir virðast þar af leiðandi blárri. Kaldari hlutir geisla mest frá sér á löngum bylgjulengdum; þeir virðast þar af leiðandi rauðari.

Samkvæmt lögmáli Wiens er bylgjulengd hámarksútgeislunar svarthlutar í öfugu hlutfalli við hitastigið í kelvin. Með öðrum orðum, ef hitastig svarthlutar tvöfaldast, helmingast bylgjulengd hámarksútgeislunar. Þannig er bylgjulengd hámarksútgeislunar svarthlutar með hitastigið 6000 K, 480 nm (λ_max = (0,0029 K · m)/(6000K) = 4,8 x 10^-7 m = 480 nm) í sýnilega hluta rafsegulrófsins. Við 12.000 K eða tvöfalt hitastig er bylgjulengd hámarksútgeislunar svarthlutar helmingi minna eða λ_max = 240 nm, sem er í útfjólubláa hluta rafsegulrófsins. Við 3000 K er bylgjulengd hámarksútgeislunar svarthlutar 960 nm, sem er í innrauða hluta rafsegulrófsins. Eins og sjá má eru bylgjulengdirnar í fullkomnu samræmi við hápunkt ferilsins.

Lögmál Wiens er sérstaklega gagnlegt til að finna út yfirborðshitastig stjarna. Hvorki er nauðsynlegt að þekkja fjarlægð stjörnunnar né hve stór hún er eða hversu mikla orku hún geislar frá sér. Allt sem þarf er aðalbylgjulengd stjörnunnar.

3.2. Lögmál Stefan-Boltzmann

Önnur gagnleg formúla fyrir svarthlutageislun felur í sér heildarmagn þeirrar orku sem svarthluturinn geislar frá sér á öllum bylgjulengdum. Ferlarnir á myndinni fyrir ofan sýnir hversu mikilli orku svarthlutur geislar frá sér á hverri bylgjulengd.

Orka er venjulega mæld í júlum (joule, J), einingu sme nefnt er eftir enska eðlisfræðingnum James Joule. Júl er orka tveggja kílógramma massa sem hreyfist með 1 metra hraða á sekúndu. Júl er þægileg orkueining því hún er nátengd einingunni fyrir afl sem er watt (W). 1 watt er 1 júl á sekúndu, eða 1 w = 1 J/s. Þannig notar t.a.m. 100 watta ljósapera 100 júl á sekúndu eða 100 J/s.

Orkumagnið sem svarthlutur gefur frá sér veltur bæði á hitastiginu og yfirborðsflatarmálinu. Þetta er augljóst: Stór brennandi eldiviður gefur frá sér miklu meiri varma og ljós heldur en glóandi eldspýta, jafnvel þótt hitastigið sé það sama. Til að skoða áhrif hitastigsins einvörðungu er þægilegt að líta á orkumagnið sem berst frá hverjum fermetra af yfirborði hlutar á sekúndu. Þetta magn kallast orkuflæði (energy flux) sem mælir hversu hratt orka berst út frá fyrirbæri. Orkuflæðið er mælt í júlum á fermetra á sekúndu, skrifað J/m²/s. 1 watt = 1 júl á sekúndu svo við getum skrifað orkuflæðið í wöttum á fermetra (W/m²).

Írski nítjándu aldar eðlisfræðingurinn David Tyndall gerði fyrstu nákvæmu mælingarnar á magni geislunar á svarthluti. Tyndall rannsakaði ljós frá heitum platínuvír sem hegðar sér nokkurn veginn eins og svarthlutur. Slóvenski eðlisfræðingurinn Josef Stefan rannsakaði niðurstöður Tyndalls árið 1879 og komst að því að orkuflæðið frá svarthlut er í hlutfalli við hitastigi fyrirbærisins (mælt í kelvin) í fjórða veldi. Fimm árum síðar sýndi austurríski eðlisfræðingurinn Ludwig Boltzmann hvernig hægt var að leiða lögmálið stærðfræðilega út frá grunnályktunum um atóm og sameindir. Af þessari ástæðu er lögmál Stefans venjulega nefnd lögmál Stefan-Boltzmann:

\Phi = \sigma T^4

þar sem Φ = orkuflæði í júlum á fermetra á sekúndu (Φ er gríski bókstafurinn fí), σ = Stefan-Boltzmann fasti = 5,67 x 10^-8 W m^-2 K^-4T = hitastig hlutar í kelvingráðum

Gildi Stefan-Boltzmann fastans σ (sigma) er fundinn með tilraunum.

Lögmál Stefan-Boltzmann segir að ef hitastig hlutar tvöfaldast (t.d. úr 300 K í 600 K) eykst orkan, sem geislar út frá hverjum fermetra á yfirboðrinu á hverri sekúndu, sextánfalt (2⁴ = 16). Við aukum hitastigið tífalt (t.d. úr 300 K í 3000 K) eykst orkuútgeislunin frá yfirborðinu á hverri sekúndu 10.000 falt (10⁴ = 10.000). Þess vegna gefur járnbiti við stofuhita frá sér frekar litla rafsegulgeislun á meðan 3000 K heitur járnbiti glóir umtalsvert.

4. Tilkoma skammtafræðinnar

Undir lok nítjándu aldar gerðu eðlisfræðingar sér vonir um að útskýra öll einkenni svarthlutageislunar. Að því leytinu til smíðuðu þeir kenningar út frá lýsingu Maxwells á ljósi sem rafsegulbylgju. Allar slíkar kenningar gátu ekki útskýrt lögun svarthlutaferlanna. Árið 1900 tókst þýska eðlisfræðingnum Max Planck að leiða út formúlu út frá lögmáli Wiens sem lýsti á réttan hátt svarthlutaferli. Fimm árum síðar komst enn annar þýskur eðlisfræðingur, Albert Einstein, að því að þessi kenning Plancks dró upp nýja og byltingarkennda mynd af eðli ljóss. Þessi nýja mynd sýndi að rafsegulgeislun losnar í litlum orkuskömmtum. Var þetta upphafið að skammtafræðinni.

Sjá nánar: Ljósið

Heimildir:

1. Christensen, Lars Lindberg; Fosbury, Robert; Hurt, Robert. 2009. Hidden Universe. Wiley-VCH Verlag, Weinheim, Þýskalandi.
2. Christensen, Lars Lindberg og Schilling, Govert. 2009. Eyes on the Skies: 400 Years of Telescopic Discovery. Wiley-VCH Verlag, Weinheim, Þýskalandi.
3. Freedman, Roger og Kaufmann, William. 2004. Universe, 8th Edition. W. H. Freeman, New York.

Hvernig vitna skal í þess grein

• Sævar Helgi Bragason (2010). Svarthlutargeislun. Stjörnufræðivefurinn. http://stjornuskodun.is/svarthlutargeislun (sótt: DAGSETNING)